Let f(x) = and
g(x)=
Show that f'(x) = g'(x) for all x domains. Can we conclude from...

Mathematics, 29.07.2021 18:50 ozheng24112
Let f(x) = 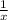 and
g(x)=
and
g(x)= 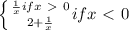
Show that f'(x) = g'(x) for all x domains. Can we conclude from the corollary below that f-g is constant?
[If f'(x) = g'(x) for all x in an interval (a, b) then f - g is constant on (a, b); that is, f(x) = g(x) + c where c is a constant.
fins f'(x) and g'(x)

Answers: 1
Another question on Mathematics

Mathematics, 21.06.2019 17:30
If you apply the below transformations to the square root parent function, f(x) = vx, what is the equation of the new function? • shift 12 units right. • shift seven units down.
Answers: 1

Mathematics, 21.06.2019 18:00
Jose predicted that he would sell 48 umbrellas. he actually sold 72 umbrellas. what are the values of a and b in the table below? round to the nearest tenth if necessary
Answers: 2

Mathematics, 21.06.2019 18:50
The random variable x represents the number of phone calls an author receives in a day, and it has a poisson distribution with a mean of 8.7 calls. what are the possible values of x
Answers: 1

You know the right answer?
Questions

History, 23.01.2021 18:30


Mathematics, 23.01.2021 18:30




Mathematics, 23.01.2021 18:30

Mathematics, 23.01.2021 18:30

English, 23.01.2021 18:30


English, 23.01.2021 18:30

Computers and Technology, 23.01.2021 18:30

Chemistry, 23.01.2021 18:30



Mathematics, 23.01.2021 18:40




Mathematics, 23.01.2021 18:40