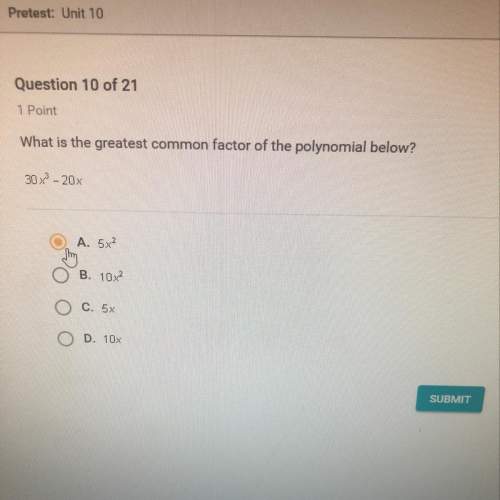
Mathematics, 07.06.2021 20:40 kadinmorgan
Jonas has 1728 copies of a 1 × 1 × 1 cube with the net
shown, where c is a positive integer and c < 100. Using
these 1728 cubes, Jonas builds a large 12×12×12 cube in
such a way that the sum of the numbers on the exterior
faces is as large as possible. For some values of c, the sum
of the numbers on the exterior faces is between 80 000 and
85 000. The number of such values of c is
(A) 39 (B) 38 (C) 37
(D) 36 (E) 35

Answers: 2
Another question on Mathematics

Mathematics, 21.06.2019 14:00
30 in the diagram line e and made parallel to each other and line p and q are transversal. use properties of special angles formed by parallel lines and their transversals to find the missing angle measures. m< 3=65 m< 15=120 m< 7= m< 4= m< 6= m< 1= m< 16= m< 18= m< 21= m< 10= m< 11= m< 12=
Answers: 1

Mathematics, 21.06.2019 15:10
5.(04.07) two different plants grow each year at different rates, which are represented by the functions f(x) = 4* and g(x) = 5x + 2. what is the first year the f(x) height is greater than the g(x) height? year 3 year 0 year 2 year 1
Answers: 1

Mathematics, 21.06.2019 22:00
The birth weights of newborn babies in the unites states follow in a normal distrubution with a mean of 3.4 kg and standard deviation of 0.6 kg. reaserches interested in studying how. children gain weights decide to take random samples of 100 newborn babies and calculate the sample mean birth weights for each sample
Answers: 1

Mathematics, 21.06.2019 23:00
Someone answer this asap for the first five terms of a sequence are shown. 5, 11, 23, 47, 95, . . which recursive function defines the nth term in the sequence for n > 1? a. f(n) = f(n - 1) + 6 b) f(n) = f(n - 1) + 48 c) f(n) = 3 • f(n - 1) + 1 d) f(n) = 3 • f(n - 1) - 4
Answers: 1
You know the right answer?
Jonas has 1728 copies of a 1 × 1 × 1 cube with the net
shown, where c is a positive integer and c &...
Questions


Computers and Technology, 29.07.2020 20:01


English, 29.07.2020 20:01


Mathematics, 29.07.2020 20:01


Physics, 29.07.2020 20:01