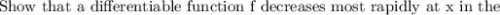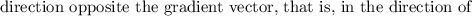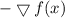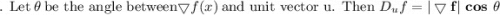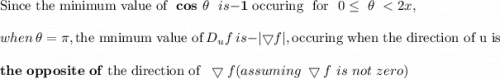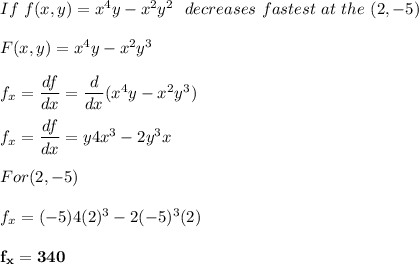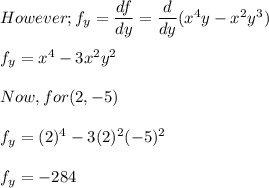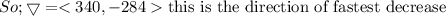Mathematics, 26.03.2021 22:10 meaddestinee
(a) Show that a differentiable function f decreases most rapidly at x in the direction opposite the gradient vector, that is, in the direction of −∇f(x). Let θ be the angle between ∇f(x) and unit vector u. Then Du f = |∇f| cos θ . Since the minimum value of cos θ is -1 occurring, for 0 ≤ θ < 2π, when θ = , the minimum value of Du f is −|∇f|, occurring when the direction of u is the opposite of the direction of ∇f (assuming ∇f is not zero). (b) Use the result of part (a) to find the direction in which the function f(x, y) = x4y − x2y3 decreases fastest at the point (2, −5).

Answers: 3
Another question on Mathematics

Mathematics, 21.06.2019 15:00
Mustafa contributes 11% of his $67,200 annual salary to his 401k plan. what is his pretax income
Answers: 1

Mathematics, 21.06.2019 20:00
Consider the set of all four-digit positive integers less than 2000 whose digits have a sum of 24. what is the median of this set of integers?
Answers: 1

Mathematics, 21.06.2019 21:00
If there are 3.281 feet in 1 meter, how many inches are in one centimeter
Answers: 1

Mathematics, 21.06.2019 21:30
The measures of the legs of a right triangle are 15m and 20m . what is the length of the hypotenuse
Answers: 1
You know the right answer?
(a) Show that a differentiable function f decreases most rapidly at x in the direction opposite the...
Questions

Social Studies, 30.11.2019 01:31


Mathematics, 30.11.2019 01:31




Mathematics, 30.11.2019 01:31










English, 30.11.2019 01:31


Computers and Technology, 30.11.2019 01:31

Mathematics, 30.11.2019 01:31