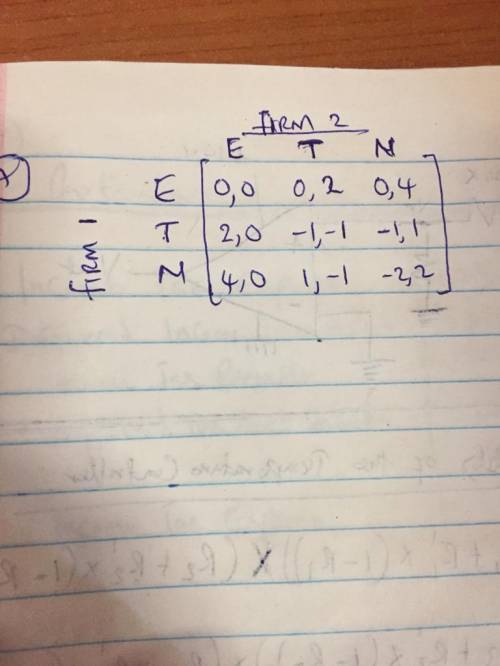Mathematics, 08.03.2021 20:10 milkshakegrande101
Consider two competing firms in a declining industry that cannot support both firms profitably. Each firm has three possible choices, as it must decide whether or not to exit the industry immediately, at the end of this quarter, or at the end of the next quarter. If a firm chooses to exit then its payoff is 0 from that point onward. Each quarter that both firms operate yields each a loss equal to -1, and each quarter that a firm operates alone yields it a payoff of 2. For example, if firm 1 plans to exit at the end of this quarter while firm 2 plans to exit at the end of next quarter then the payoffs are 1,1) because both firms lose -1 in the first quarter and firm 2 gains 2 in the second. The payoff for each firm 1.
a. Write down this game in matrix form
b. Are there any strictly dominated strategies? Are there any weakly dominated strategies?
c. Find the pure-strategy Nash Equilibria.
d. Find the unique mixed-strategy Nash equilibrium.

Answers: 3
Another question on Mathematics

Mathematics, 20.06.2019 18:04
The parking lot of a store has the shape shown. all angles are right angles. what is the area of the parking lot?
Answers: 3

Mathematics, 21.06.2019 13:30
Ben wants to play a carnival game that costs $2. in his pocket he has 5 red tickets worth 35 cents each, and 15 blue tickets worth 10 cents each. which of the following systems of inequalities correctly represents the constraints on the variables in this problem? let represent the red tickets and b represent the blue tickets.
Answers: 2

Mathematics, 21.06.2019 17:00
Asays "we are both knaves" and b says nothing. exercises 24–31 relate to inhabitants of an island on which there are three kinds of people: knights who always tell the truth, knaves who always lie, and spies (called normals by smullyan [sm78]) who can either lie or tell the truth. you encounter three people, a, b, and c. you know one of these people is a knight, one is a knave, and one is a spy. each of the three people knows the type of person each of other two is. for each of these situations, if possible, determine whether there is a unique solution and determine who the knave, knight, and spy are. when there is no unique solution, list all possible solutions or state that there are no solutions. 24. a says "c is the knave," b says, "a is the knight," and c says "i am the spy."
Answers: 2

Mathematics, 21.06.2019 17:00
Use the frequency distribution, which shows the number of american voters (in millions) according to age, to find the probability that a voter chosen at random is in the 18 to 20 years old age range. ages frequency 18 to 20 5.9 21 to 24 7.7 25 to 34 20.4 35 to 44 25.1 45 to 64 54.4 65 and over 27.7 the probability that a voter chosen at random is in the 18 to 20 years old age range is nothing. (round to three decimal places as needed.)
Answers: 1
You know the right answer?
Consider two competing firms in a declining industry that cannot support both firms profitably. Each...
Questions

Mathematics, 29.04.2021 04:10

Mathematics, 29.04.2021 04:10



Mathematics, 29.04.2021 04:10

Social Studies, 29.04.2021 04:10

Mathematics, 29.04.2021 04:10

Mathematics, 29.04.2021 04:10



Mathematics, 29.04.2021 04:10




Mathematics, 29.04.2021 04:10

Mathematics, 29.04.2021 04:10

English, 29.04.2021 04:10



Mathematics, 29.04.2021 04:10