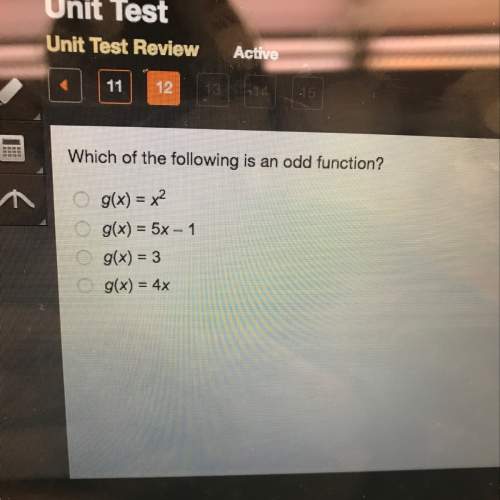
Mathematics, 01.02.2021 07:10 SuperLegend
Let X be a topological space and let C and U be subsets of X. Define C to be closed if C contains all its limit points and define U to be open if every point p ∈ U has a neighborhood which is contained in U. Assuming these definitions show that the following statements are equivalent for a subset S of X. i) S is closed in X; ii) X – S is open in X; iii) S = [S].

Answers: 2
Another question on Mathematics

Mathematics, 21.06.2019 17:30
Which of the following equations is of the parabola whose vertex is at (2, 3), axis of symmetry parallel to the y-axis and p = 4? a.)y-3 = 1/16 (x-2)^2 b.)y+3 = -1/16 (x+2)^2 c.)x-2 = 1/16 (y-3)^2
Answers: 3


Mathematics, 22.06.2019 00:00
240 seventh graders and two-thirds of the students participate in after-school activities how many students participate in after-school activities
Answers: 1

Mathematics, 22.06.2019 03:00
Use matrices to solve this linear system: 5x1 − 2x2 = −30 2x1 − x2 = −13 x1 = x2 =
Answers: 2
You know the right answer?
Let X be a topological space and let C and U be subsets of X. Define C to be closed if C contains al...
Questions

Mathematics, 23.07.2019 08:00


History, 23.07.2019 08:00


Arts, 23.07.2019 08:00


Social Studies, 23.07.2019 08:00



Biology, 23.07.2019 08:00

Mathematics, 23.07.2019 08:00




Social Studies, 23.07.2019 08:00


English, 23.07.2019 08:00

Mathematics, 23.07.2019 08:00

History, 23.07.2019 08:00

Mathematics, 23.07.2019 08:00