Mathematics, 26.01.2021 23:50 alisonmrodriquez1450
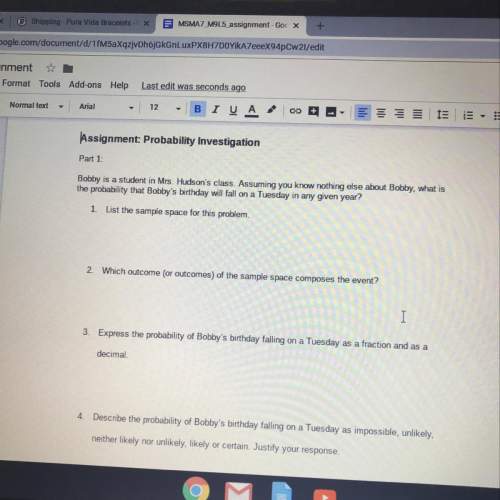
Let X be a topological space and let C and U be subsets of X. Define C to be closed if C contains all its limit points and define U to be open if every point p ∈ U has a neighborhood which is contained in U. Assuming these definitions show that the following statements are equivalent for a subset S of X. i) S is closed in X; ii) X – S is open in X; iii) S = [S].

Answers: 1
Another question on Mathematics

Mathematics, 21.06.2019 16:00
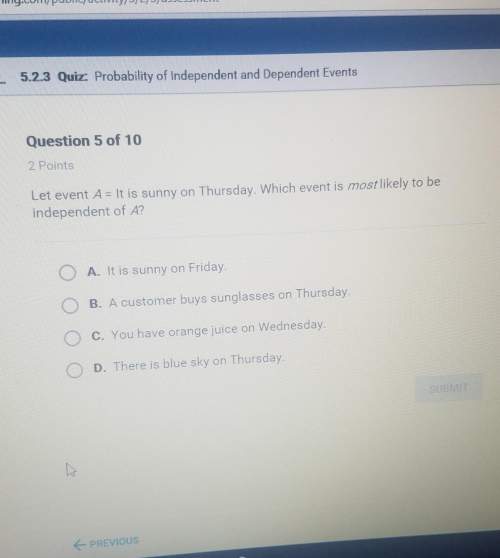
Drag the tiles to the correct boxes to complete the pairs. not all tiles will be used. the heights of the girls in an advanced swimming course are 55, 60, 59, 52, 65, 66, 62, and 65 inches. match the measures of this data with their values.
Answers: 1

Mathematics, 21.06.2019 18:00
Olga used 100 ounces of flour to make 225 muffins. how many ounces of flour will be used to make 300 muffins?
Answers: 2

Mathematics, 21.06.2019 20:30
8. kelly wants to buy a magazine that is $25. later the magazine was marked up an additional 20%. what is the new price?
Answers: 1

Mathematics, 21.06.2019 21:10
Which exponential function has an initial value of 2? f(x) = 2(3x) f(x) = 3(2x)
Answers: 1
You know the right answer?
Let X be a topological space and let C and U be subsets of X. Define C to be closed if C contains al...
Questions

History, 06.07.2019 05:30

Mathematics, 06.07.2019 05:30


History, 06.07.2019 05:30

Mathematics, 06.07.2019 05:30

History, 06.07.2019 05:30



Biology, 06.07.2019 05:30



Mathematics, 06.07.2019 05:30

Mathematics, 06.07.2019 05:30

History, 06.07.2019 05:30

Social Studies, 06.07.2019 05:30



English, 06.07.2019 05:30

Mathematics, 06.07.2019 05:30