
Mathematics, 16.10.2020 06:01 rodrickahammonds
Consider the problem of utility over territory. Let’s start simply
with a one-dimensional representation. Consider two actors, 1
and 2, with utility functions defined over a single-dimensional
issue space X = [0, 1], but where the actors can own sections or
“provinces” of the interval. The boundaries between sections are
defined by a vector B = (b1, b2, b3, . . . , bn, 1).
Thus, there are n+ 1 provinces. Define a “size” vector containing the lengths of
each province, S = (b1, b2 − b1, b3 − b2, . . . , 1 − bn). Define for
each actor an “ownership” vector Oi with 1s in the place of the
provinces that it owns and 0s elsewhere.
1. Assume that each actor’s utility function is a simple sum of
how much of the space they own so ui=∑n+1,j=1, oj, sj
(a) Can the players both be made better off by exchanging
existing provinces?
(b) Can the players both be made better off by altering the
boundaries of the existing provinces while preserving the
ownership structure?
(c) Can the players both be made better off by reducing the
number of provinces – for instance, by consolidating
contiguous provinces that are owned by the same actor?
2. Now assume that the utility function is a function of the sum
of the squares of the provinces owned, indicating that there are
increasing returns to the size of a province ui=∑n+1,j=1, (oj, sj)^2
(a) Can the players both be made better off by exchanging
existing provinces (without doing anything else)?
(b) Can the players both be made better off by reducing the
number of provinces – for instance, by consolidating
contiguous provinces that are owned by the same actor?
(c) If the actors are free to adjust both the number of
provinces and the ownership structure, what set of
boundaries is Pareto optimal with this utility function?
2.2 (see formula in the attachments) Consider two states, state 1 and state 2, which can unilaterally
set their tariff rates on imported goods, ti ≥ 0. Each state has an
ideal level for its own tariff, and prefers that the other
side’s tariff be 0, Assume that each side’s utility declines
with the distance between the tariff levels and their ideal point,
as follows
1. Draw the t1, t2 quadrant and draw in the ideal points for each
player.
2. Draw in sample indifference curves for the two states around
their ideal points. What shape are they?
3. Draw in the contract curve between the two ideal points. What
shape is it and why? What equation describes it?
4. The contract curve divides the t1, t2 quadrant into two regions.
How do they differ in terms of how the players could realize
joint gains in each region?
2.3 Consider the utility function u(x) = xρ, where ρ > 0 and x ∈ [0,
1]. Under what conditions would a player with such preferences
be risk acceptant, risk neutral, and risk averse?
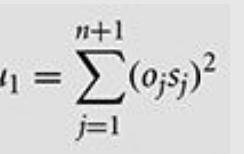

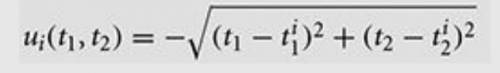

Answers: 1
Another question on Mathematics

Mathematics, 21.06.2019 19:40
Which of the following could be the ratio of the length of the longer leg 30-60-90 triangle to the length of its hypotenuse? check all that apply. a. 313 6 b. 3: 215 c. 18: 13 d. 1: 13 e. 13: 2 of. 3: 15
Answers: 3


Mathematics, 21.06.2019 22:20
Which strategy is used by public health to reduce the incidence of food poisoning?
Answers: 1

You know the right answer?
Consider the problem of utility over territory. Let’s start simply
with a one-dimensional represent...
Questions



Mathematics, 09.07.2019 02:00




History, 09.07.2019 02:00

English, 09.07.2019 02:00



Mathematics, 09.07.2019 02:00

Chemistry, 09.07.2019 02:00

Mathematics, 09.07.2019 02:00




Chemistry, 09.07.2019 02:00

English, 09.07.2019 02:00

History, 09.07.2019 02:00



