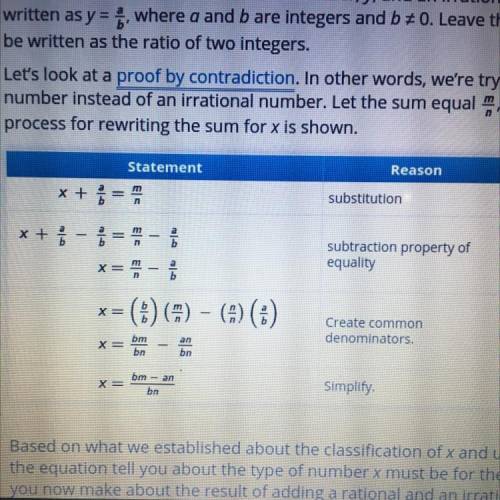
Part D Now examine the sum of a rational number, y, an an irrational number, x. The
rational number y can be written as y=a/b, where a and b are integers and b≠0. Leave the irrational number x as x because it can’t be written as the ratio of two integers.
Let’s look at a proof by contradiction. In other words, we’re trying to show that x+y is equal to a rational number instead of an irrational number. Let the sum equal m/n, where m and n are integers and n≠0. The process for writing the sum for x is shown.

Based on what we established about the classification of x and using the closure of integers, what does the equation tell you about the type of number x and must be for the sum to be rational? What conclusion can you now make about the result of adding a rational and an irrational number?

iu

step-by-step explanation:

answer: the first graph

step-by-step explanation:

ratios represent a pattern or relationship that can be scaled.

equivalent ratios are pairs of ratios that represent the same relationship between quantities, and can be generated by multiplying or dividing both quantities in the ratio by the same factor.

in this lesson, students will use double number lines and ratio reasoning to solve ratio problems. by partitioning double number lines into proportionate intervals, students will build an understanding of equivalent ratio relationships as those that are generated by multiplying or dividing two related quantities by the same number. this lesson will build upon students' prior understanding of multiplicative comparisons, number line reasoning and equivalent fractions (while highlighting the difference between equivalent fractions and equivalent ratios); and will build toward future work in this unit on building ratio tables, and work in future grades in proportionality, scaling, and expressing and graphing linear functions.

step-by-step explanation:

ratios represent a pattern or relationship that can be scaled.

equivalent ratios are pairs of ratios that represent the same relationship between quantities, and can be generated by multiplying or dividing both quantities in the ratio by the same factor.

in this lesson, students will use double number lines and ratio reasoning to solve ratio problems. by partitioning double number lines into proportionate intervals, students will build an understanding of equivalent ratio relationships as those that are generated by multiplying or dividing two related quantities by the same number. this lesson will build upon students' prior understanding of multiplicative comparisons, number line reasoning and equivalent fractions (while highlighting the difference between equivalent fractions and equivalent ratios); and will build toward future work in this unit on building ratio tables, and work in future grades in proportionality, scaling, and expressing and graphing linear functions.

2

step-by-step explanation: