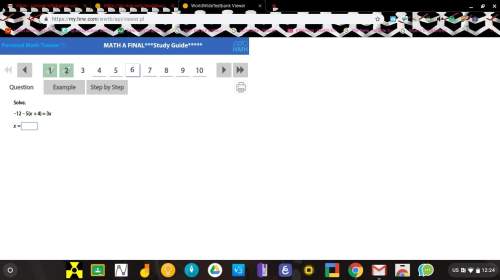
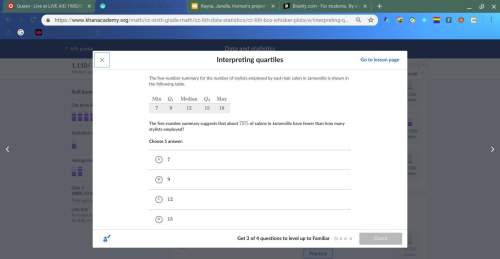
Mathematics, 21.04.2020 19:35 alisonlebron15
Consider A ∈ Mat3×3(R) and the vector v ∈R3 such that A3v = 0, but A2v 6= 0, (a) Show that the vectors A2v, Av, and v form a basis of R3. Hint: It is sufficient to show they are linearly independent. Set up the proper equation, and multiply by A2. (b) Find the matrix of the transformation T(x) = Ax with respect to the basis {A2v, Av, v}.

Answers: 2
Another question on Mathematics


Mathematics, 21.06.2019 23:30
Hundred and tens tables to make 430 in five different ways
Answers: 1

Mathematics, 22.06.2019 04:30
Write a linear funtion f with the values f(2)=-1, and f(5)=4
Answers: 2

Mathematics, 22.06.2019 05:30
Anya is making throw pillows and is choosing the type of filling and type of fabric pattern. complete each statement below about the pillow options.
Answers: 3
You know the right answer?
Consider A ∈ Mat3×3(R) and the vector v ∈R3 such that A3v = 0, but A2v 6= 0, (a) Show that the vecto...
Questions


English, 08.04.2021 22:50




Mathematics, 08.04.2021 22:50




English, 08.04.2021 22:50

Biology, 08.04.2021 22:50


Mathematics, 08.04.2021 22:50

Mathematics, 08.04.2021 22:50

Mathematics, 08.04.2021 22:50


English, 08.04.2021 22:50


Mathematics, 08.04.2021 22:50

Social Studies, 08.04.2021 22:50