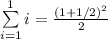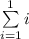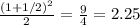Mathematics, 15.04.2020 03:26 smithad382
What is wrong with this "proof"? "Theorem" For every positive integer n, n i =1 i = (n + 1 2 ) 2 /2. Basis Step: The formula is true for n = 1. Inductive Step: Suppose thatn i=1 i = (n + 1 2 ) 2 /2. Then n+1 i=1 i = ( n i=1 i) + (n + 1). By the induc-tive hypothesis, n+1 i=1 i = (n + 1 2 ) 2 /2 + n + 1 = (n 2 + n + 1 4 )/2 + n + 1 = (n 2 + 3n + 9 4 )/2 = (n + 3 2 ) 2 /2 =[ (n + 1) + 1 2 ] 2 /2, completing the induc-tive step.

Answers: 1
Another question on Mathematics

Mathematics, 21.06.2019 14:00
Emma will roll two number cubes labeled 1 through 6. she will record the sum of the two numbers after each roll. she will roll the two cubes 540 times. how many times should emma expect the sum to equal 5?
Answers: 2


Mathematics, 21.06.2019 22:00
18 16 11 45 33 11 33 14 18 11 what is the mode for this data set
Answers: 2

Mathematics, 22.06.2019 00:00
Asequence has a common ratio of and f(5) = 81. which explicit formula represents the sequence? f(x) = 24 f(x) = 16 f(x) = 24 f(x) = 16
Answers: 1
You know the right answer?
What is wrong with this "proof"? "Theorem" For every positive integer n, n i =1 i = (n + 1 2 ) 2 /2....
Questions

Advanced Placement (AP), 14.01.2021 03:00

Mathematics, 14.01.2021 03:00



Mathematics, 14.01.2021 03:00


History, 14.01.2021 03:00




Physics, 14.01.2021 03:00

History, 14.01.2021 03:00

Biology, 14.01.2021 03:00


Mathematics, 14.01.2021 03:00

Mathematics, 14.01.2021 03:00


Mathematics, 14.01.2021 03:00

Health, 14.01.2021 03:00