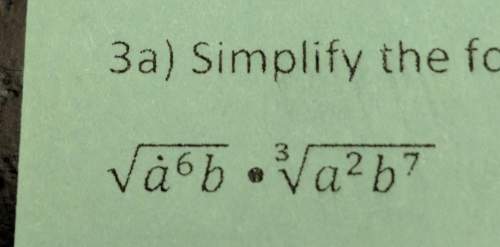Mathematics, 28.12.2019 18:31 robert7248
Find a power series for f(x)=xln(1+x). \[f(x)=xln(1+x)\]. \[\frac{d}{dx}xln(1+x)\]. \[=\frac{x}{x+1}+ln(x+1)\]. \[=\sum_{n=0}^{\infty}(-1)^nx^n+\fr ac{d}{dx}ln(x+1)\]. \[\sum_{n=0}^{\infty}(-1)^nx^n+\sum _{n=0}^{\infty}(-1)^n\frac{x^{n+1}} {n+1}\]

Answers: 2
Another question on Mathematics

Mathematics, 21.06.2019 14:00
Arandom number generator is used to model the patterns of animals in the wild this type of study is called
Answers: 1

Mathematics, 21.06.2019 16:20
To prove that def ~ gfh by the sss similarity theorem using the information provided in the diagram, it would be enough additional information to know that
Answers: 3

Mathematics, 21.06.2019 17:30
Danielle earns a 7.25% commission on everything she sells at the electronics store where she works. she also earns a base salary of $750 per week. what were her sales last week if her total earnings for the week were $1,076.25?
Answers: 3

Mathematics, 21.06.2019 20:00
The function models the number of accidents per 50 million miles driven as a function
Answers: 1
You know the right answer?
Find a power series for f(x)=xln(1+x). \[f(x)=xln(1+x)\]. \[\frac{d}{dx}xln(1+x)\]. \[=\frac{x}{x+1}...
Questions



Health, 22.08.2019 21:30

Engineering, 22.08.2019 21:30

History, 22.08.2019 21:30

Biology, 22.08.2019 21:30



English, 22.08.2019 21:30


Biology, 22.08.2019 21:30



Mathematics, 22.08.2019 21:30

Mathematics, 22.08.2019 21:30

World Languages, 22.08.2019 21:30

Geography, 22.08.2019 21:30

Mathematics, 22.08.2019 21:30

Mathematics, 22.08.2019 21:30

Biology, 22.08.2019 21:30