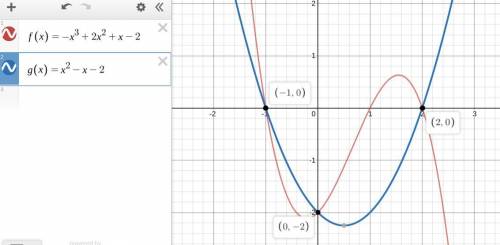
Ros is trying to find the solution(s) to the system {f(x)=−x3+2x2+x−2g(x)=x2−x−2.
roz wan...

Mathematics, 25.01.2020 12:31 marialion5278
Ros is trying to find the solution(s) to the system {f(x)=−x3+2x2+x−2g(x)=x2−x−2.
roz wants to find the solution(s) to this system. after analyzing the graph of the functions, roz comes up with the following list ordered pairs as possible solutions: (0,−2), (2,0), and (−1,0).
which work correctly verifies whether each of roz’s ordered pairs is a solution?
a. a solution to the system will be the intersection of f(x) and g(x) such that f(x)=g(y). roz must verify one of the following: f(0)=g(−2) and f(−2)=g(0); f(2)=g(0) and f(0)=g(2), or f(−1)=g(0) and f(0)=g(−1).
1. f(0)=−03+2(02)+0−2=−2; g(−2)=(−2)2−2−2=0 thus, (0,−2) is a solution.
2. f(2)=−23+2(22)+2−2=0; g(0)=02−0−2=2 thus, (2,0) is a solution.
3. f(−1)=−(−1)3+2(−1)2+(−1)−2=0; g(0)=02−0−2=2 thus, (−1,0) is not a solution.
b. a solution to the system will be the intersection of f(x) and g(x) such that f(x)=g(x). roz must verify that f(0)=g(0)=−2, f(2)=g(2)=0, and f(−1)=g(−1)=0 as follows:
1. f(0)=−03+2(02)+0−2=−2; g(0)=02−0−2=−2 thus, (0,−2) is a solution.
2. f(2)=−23+2(22)+2−2=0; g(2)=22−2−2=0 thus, (2,0) is a solution.
3. f(−1)=−(−1)3+2(−1)2+(−1)−2=0; g(−1)=(−1)2−(−1)−2=0 thus, (−1,0) is a solution.
c. a solution to the system will be the intersection of f(x) and g(x) such that f(x)=g(x). roz must verify that f(−2)=g(−2)=0, and f(0)=g(0)=2 or f(0)=g(0)=−1 as follows:
1. f(−2)=−23+2(22)+2−2=0; g(−2)=(−2)2−2−2=0 thus, (0,−2) is a solution.
2. f(0)=−03+2(02)−0+2=2; g(0)=02−0−2=2 thus, (2,0) is a solution.
3. since f(0)=g(0)=2, f(0) and g(0) cannot equal −1. thus, (−1,0) is not a solution.
d. a solution to the system will be the intersection of f(x) and g(x) such that f(x)=g(x). roz must verify that f(−2)=g(−2)=0, and f(0)=g(0)=2 or f(0)=g(0)=−1 as follows:
1. f(−2)=−23+2(22)+2−2=0; g(−2)=(−2)2−2−2=0 thus, (0,−2) is a solution.
2. f(0)=−03+2(02)−0+2=2; g(0)=02−0−2=2 thus, (2,0) is a solution.
since f(0)=g(0)=2, f(0) and g(0) cannot equal −1. thus, (−1,0) is not a solution.

Answers: 2
Another question on Mathematics

Mathematics, 21.06.2019 18:30
Ricky takes out a $31,800 student loan to pay his expenses while he is in college. after graduation, he will begin making payments of $190.66 per month for the next 30 years to pay off the loan. how much more will ricky end up paying for the loan than the original value of $31,800? ricky will end up paying $ more than he borrowed to pay off the loan.
Answers: 1

Mathematics, 21.06.2019 19:20
Which of the following quartic functions has x = –1 and x = –2 as its only two real zeroes?
Answers: 1

Mathematics, 21.06.2019 20:00
What is the x-intercept and y-intercept of the equation 2x+1. 2o
Answers: 2

Mathematics, 21.06.2019 20:30
How do you determine if an ordered pair is a solution to a given equation?
Answers: 1
You know the right answer?
Questions


History, 05.05.2020 10:26

Biology, 05.05.2020 10:26


Physics, 05.05.2020 10:26


Mathematics, 05.05.2020 10:26

History, 05.05.2020 10:26

Physics, 05.05.2020 10:26

Spanish, 05.05.2020 10:26


English, 05.05.2020 10:27

Computers and Technology, 05.05.2020 10:27

World Languages, 05.05.2020 10:27

Mathematics, 05.05.2020 10:27


English, 05.05.2020 10:27



Mathematics, 05.05.2020 10:27