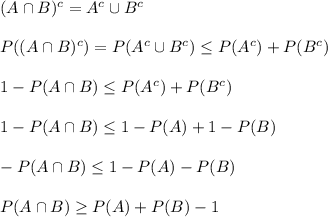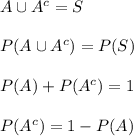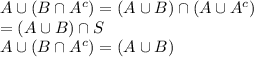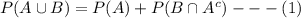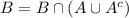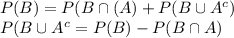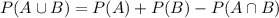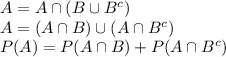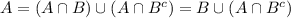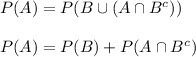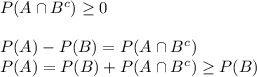For two events a and b show that p (a∩b) ≥ p (a)+p (b)−1.
(hint: apply de morgan’s law...

Mathematics, 10.01.2020 03:31 stacy021603
For two events a and b show that p (a∩b) ≥ p (a)+p (b)−1.
(hint: apply de morgan’s law and then the bonferroni inequality).
derive below results 1 to 4 from axioms 1 to 3 given in section 2.1.2 in the textbook.
result 1: p (ac) = 1 − p(a)
result 2 : for any two events a and b, p (a∪b) = p (a)+p (b)−p (a∩b)
result 3: for any two events a and b, p(a) = p(a ∩ b) + p (a ∩ bc)
result 4: if b ⊂ a, thena∩b = b. therefore p (a)−p (b) = p (a ∩ bc) and p (a) p(b).

Answers: 3
Another question on Mathematics

Mathematics, 20.06.2019 18:04
Find an equation (in term of x) of line through the points (-1,3) and (1,4)
Answers: 3

Mathematics, 21.06.2019 15:30
On a architect's drawing of a house, 1 inche representa 1.5
Answers: 1

Mathematics, 21.06.2019 17:30
The graph below represents the number of dolphins in a dolphin sanctuary. select all the key features of this function.
Answers: 2

Mathematics, 21.06.2019 18:20
Choose all that apply. select all of the fees a credit card may have. annual fee apr balance transfer fee cash advance fee late fee overdraft fee over-the-limit fee
Answers: 2
You know the right answer?
Questions

English, 11.10.2020 21:01


World Languages, 11.10.2020 21:01

Mathematics, 11.10.2020 21:01


History, 11.10.2020 21:01

Social Studies, 11.10.2020 21:01


Mathematics, 11.10.2020 21:01

History, 11.10.2020 21:01








Physics, 11.10.2020 21:01

Mathematics, 11.10.2020 21:01