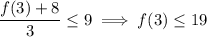Mathematics, 29.01.2020 15:02 kcarstensen59070
Example 5 suppose that f(0) = −8 and f '(x) ≤ 9 for all values of x. how large can f(3) possibly be? solution we are given that f is differentiable (and therefore continuous) everywhere. in particular, we can apply the mean value theorem on the interval [0, 3] . there exists a number c such that f(3) − f(0) = f '(c) − 0 so f(3) = f(0) + f '(c) = −8 + f '(c). we are given that f '(x) ≤ 9 for all x, so in particular we know that f '(c) ≤ . multiplying both sides of this inequality by 3, we have 3f '(c) ≤ , so f(3) = −8 + f '(c) ≤ −8 + = . the largest possible value for f(3) is .

Answers: 1
Another question on Mathematics

Mathematics, 21.06.2019 16:00
Which term best describes the association between variables a and b
Answers: 1

Mathematics, 21.06.2019 16:30
In two or more complete sentences describe how to determine the appropriate model for the set of data, (1,1), (3,2), (6,3), (11,4).
Answers: 1

Mathematics, 21.06.2019 17:00
The vet charges $45 for an office visit and $10 for each vaccination your dog needs. write an eaquation
Answers: 1

Mathematics, 21.06.2019 17:30
Adiverr from the university of florida women’s swimming and diving team is competing in the ncaa zone b championships
Answers: 2
You know the right answer?
Example 5 suppose that f(0) = −8 and f '(x) ≤ 9 for all values of x. how large can f(3) possibly be?...
Questions

History, 23.06.2019 14:30





English, 23.06.2019 14:30



Spanish, 23.06.2019 14:30

Social Studies, 23.06.2019 14:30






Mathematics, 23.06.2019 14:40

Advanced Placement (AP), 23.06.2019 14:40



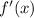 exists and is bounded for all
exists and is bounded for all  . We're told that
. We're told that 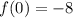 . Consider the interval [0, 3]. The mean value theorem says that there is some
. Consider the interval [0, 3]. The mean value theorem says that there is some 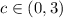 such that
such that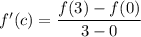
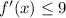 , we have
, we have